Napier’s constant: What is it and where do we use it?

Just as pi is basic in Geometry and the number “i” in Algebra and Complex Analysis, “e” is the base of natural logarithms and being part of the equations of compound interest.

It acts an important role in Calculus and an Analysis of one of the most important functions in the field of mathematics.

The exponential function e^x is a mathematical function that is used to describe the behavior of things.

The things can be:

• Chemical
• Cellular reactions
• Physical
• Electrical

It is the only function of “x” which shows a unique behavior with a rate of change.

The rate of change with respect to x is equal to the function itself in the area of the exponential function.

Simply put, when a phenomenon is expressed in exponential form, it has the property that the rate of change is directly proportional to the rate of change of its variable.

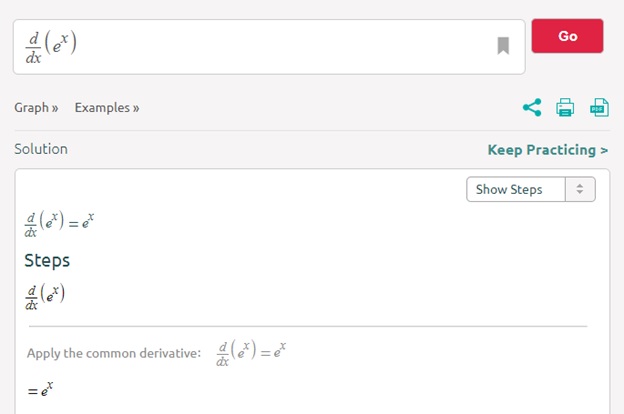
This answers why the derivative of the function e^x is the same function.

It can explain physical events controlled by simple laws, such as:

• The emptying of a sinkhole or a wind vane.
• The value of continuous compound interest used in loans and investments.

The value of Napier’s constant or e raise to power x can be easily calculated.

As the value of e is 2.71828, so you only have to put the value of x in the power and the value of Napier’s constant can be obtained.

From this, we can determine:

If x=1, then

e^x = (2.71828)¹ = 2.71828

If x=2, then

e^x = (2.71828)² = 7.38906

If x=3, then

e^x = (2.71828)³ = 20.08554

If x=4, then

e^x = (2.71828)⁴ = 54.59815

If x=5, then

e^x = (2.71828)⁵ = 148.41316

However, if the value of x is big, then the calculation can be complex.

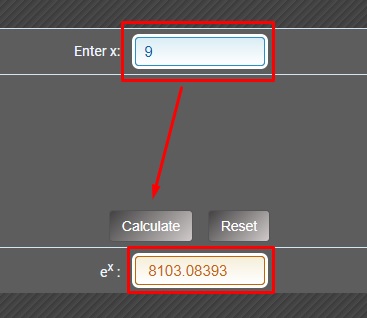
In this scenario, we can use an e power calculator to find the desired value.

By using this online free tool, you can evaluate Napier’s constant on a large value of x.

How to use an e power calculator?

The interface of this tool is very user-friendly. You can even figure out by yourself how to use it.

1. Enter the value of x in the input box.
2. Hit the ‘Calculate’ button as shown in the picture above.
3. You will get the desired output according to your input.
4. Copy the value from the result box or reset it if you want.

Where to use it?

When preparing for exams, people often get the impression that many math exercises are useless, or at least not used in daily life.

For example, knowing the square root of each number, factorization and derivative, the differential equations, the exponential function, complex numbers, logarithm, and so on.

Well, it’s hard to find the application fields of number e. Simply put, whenever we want to estimate the exponential magnitude, we use number e.

• The first use of the number e, though it had not been theorized, was to find the maximum profit by increasing the frequency of calculating the loan interest rates. This is called the compound interest method in continuous progression.
• In biology, we can measure the multiplication of living cells in an organism.
• We often use it in the field of physics and mathematical computation.
• In economics, we use it in the phenomenon of exponential growth and to calculate the interest paid continuously.

The number e is an irrational number, in other words, a number that cannot or can be stated as the accurate quotient of two whole numbers, whose number of decimal places is infinite and, consequently, these decimals are pursued without a logical sequence.

Little History

Thanks to the research work of the Scottish mathematician John Napier, the number e appeared with the development of logarithm in the 17th century.

In his reference book in 1614, Napier put forward a tool for simplifying mathematical calculations: the logarithm.

In the 17th century, computers and calculators did not exist, but that does not mean that there was no mathematical research.

In the 3rd century BC, Archimedes realized that it was enough to add the numbers and multiply them by a certain number, which was attributed to the exponent(e).

At the end of the 17th century, the number e was defined as the cardinal number of Napier’s logarithm, and then we used the following relationship to characterize it:

Ln(e) = 1

The mathematician Jacques Bernoulli was interested in using compound interest technology to find the maximum value of loan interest: by adding accumulated interest to the original deposit as much as possible, his profit can be maximized.

So, he used the e power calculation x as we have mentioned before in the “Where to use it?” section.

It was the Swiss mathematician Leonhard Euler who, a little bit later, was involved in the number e, taking its name from the initial letter of the word “exponential.”

In 1737, Euler proved the irrationality of e based on fractional continuous expansion, and resolute the expansion of e in series by factorization.

We have seen that Napier’s constant has great importance in many fields.

If you want to evaluate it in your exam, in the mathematical assignment, or to find the maximum value of loan interest, you can use an online calculator which is free.